Thuật toán sắp xếp Bubble Sort là gì? Tìm hiểu về thuật toán sắp xếp nổi bọt

Thuật toán sắp xếp nổi bọt được coi là một trong những thuật toán đơn giản nhất trong những thuật toán sắp xếp. Được sử dụng như căn bản của một lập trình viên, bạn có chắc là bạn đã nắm được toàn bộ về nó chưa? Hãy cùng bổ sung thêm những kiến thức cơ bản xung quanh sắp xếp nổi bọt này cùng chúng tôi nhé!

Thuật toán Bubble Sort là gì?

Thuật toán sắp xếp nổi bọt (Bubble Sort) hay còn có thể gọi là sắp xếp bằng so sánh trực tiếp là một thuật toán cơ bản và dễ hiểu thường được sử dụng trong những bài học mở đầu về khoa học máy tính. Bằng cách liên tục lặp lại việc so sánh hai phần tử đứng cạnh nhau và đổi chỗ chúng sao cho phù hợp với yêu cầu của bài toán, bắt đầu từ đầu hoặc cuối của dãy đến đầu còn lại cho đến khi không cần phải sắp xếp nữa, chúng ta sẽ có một dãy đã sắp xếp hoàn chỉnh. 

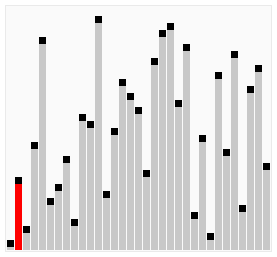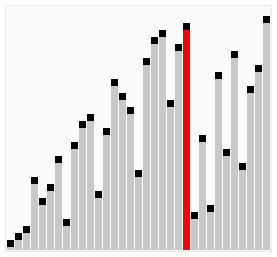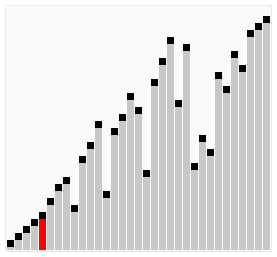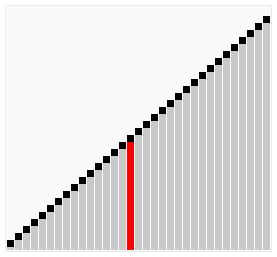
Đánh giá về thuật toán 

• Phân loại: Giải thuật sắp xếp
• Mức độ phức tạp trong trường hợp tốt: O*(n)
• Mức độ phức tạp trong trường hợp trung bình: O*(n^2)
• Thời gian xấu nhất: O*(n^2)
• Không gian bộ nhớ được sử dụng: O(1)

Ví dụ minh hoạ

Giả sử chúng ta cần sắp xếp dãy số [3 1 4 2 6] này tăng dần.

Lần lặp đầu tiên:

Đăng ký ngay

Đăng ký ngay

( 3 1 4 2 6 ) -> ( 1 3 4 2 6 ), Ở đây, thuật toán sẽ so sánh hai phần tử đầu tiên, và đổi chỗ cho nhau vì 3 > 1.

( 1 3 4 2 6 ) ->  ( 1 4 3 2 6 ), Đổi chỗ vì 3 > 4

( 1 4 3 2 6 ) ->  ( 1 4 2 3 6 ), Đổi chỗ vì 3 > 2

( 1 4 2 3 6 ) -> ( 1 4 2 3 6 ), Ở đây, hai phần tử đang xét đã đúng thứ tự (6 > 3), vậy ta không cần đổi chỗ.

Lần lặp thứ 2:

( 1 4 2 3 6 ) -> ( 1 4 2 3 6 )

( 1 4 2 3 6 ) -> ( 1 2 4 3 6 ), Đổi chỗ vì 4 > 2

( 1 2 4 3 6 ) -> ( 1 2 4 3 6 )

( 1 2 4 3 6 ) ->  ( 1 2 4 3 6 )

Đến bước này, dãy số đã được sắp xếp hoàn chỉnh. Nhưng thuật toán của chúng ta chưa thể xác nhận điều đó ngay được.Thuật toán sẽ cần sử dụng thêm một lần lặp nữa để kết luận dãy đã sắp xếp sau khi và chỉ khi lặp từ đầu đến cuối mà không phải thay đổi vị trí của bất kì phần tử nào trong dãy nữa.

Lần lặp thứ 3:

( 1 2 4 3 6 ) -> ( 1 2 4 3 6 )

( 1 2 4 3 6 ) -> ( 1 2 4 3 6 )

( 1 2 4 3 6 ) -> ( 1 2 4 3 6 )

( 1 2 4 3 6 ) -> ( 1 2 4 3 6 )

• Giải mà về thuật toán Dijkstra tìm đường đi ngắn nhất
• Quy hoạch động là gì? Tìm hiểu về thuật toán quy hoạch động

Giải thuật

Cách sắp xếp các phần tử từ trên xuống dưới:

Giả sử dãy cần phải xử lý một dãy có n phần tử. Khi chúng ta tiến hành từ trên xuống dưới, ta bắt đầu so sánh từ hai phần tử đứng đầu, nếu phần tử đứng trước lớn hơn phần tử đứng sau thì đổi chỗ cho nhau. Tiếp tục thực hiện với cặp phần tử thứ hai và thứ ba và cứ lặp lại cho đến cuối của dãy, nghĩa là so sánh phần tử đứng thứ n-1 với phần tử thứ n. Sau khi thực hiện bước này, phần tử này trở thành phần tử lớn nhất của dãy.

Sau đó, quay lại tiếp tục so sánh (và đổi chỗ nếu cần) từ hai phần tử đầu đến phần tử thứ n-2.

Cho đến khi trong một lần duyệt không cần phải đổi chỗ của bất kì cặp phần tử nào thì danh sách đã xếp xong

Cách sắp xếp từ dưới lên: 

Là sắp xếp từ cặp cuối cùng trong dãy là cặp n-1 và n, so sánh( và đổi chỗ) đến cặp đầu tiên. Sau bước này thì phần tử nhỏ nhất đã được đổi lên trên cùng.

Tính thời gian xử lý

Với mỗi i = 1,2,…,n-1 ta cần có i phép so sánh. Do đó số nhiều nhất của các lần so sánh và đổi chỗ trong giải thuật là: 

(n-1)+(n-2)+…+2+1 = ((n-1)n) / 2

Giảm bớt vòng duyệt

Nếu trong một lần duyệt với một số i cố định khi mà vòng lặp j kết thúc mà không cần đổi chỗ cặp phần tử nào thì nghĩa là mọi phần tử kề nhau đã đứng đúng thứ tự, tương đương với ta đã sắp xếp được một dãy và không cần thiết tiến hành vòng lặp tiếp theo, chúng ta có thể sử dụng một cách như sau:

procedure bubble_sort3(list L, number n)

  i:= n

  while i > 1 do

    has_swapped:= 0 //khởi tạo lại giá trị cờ

    for number j from 1 to (i – 1)

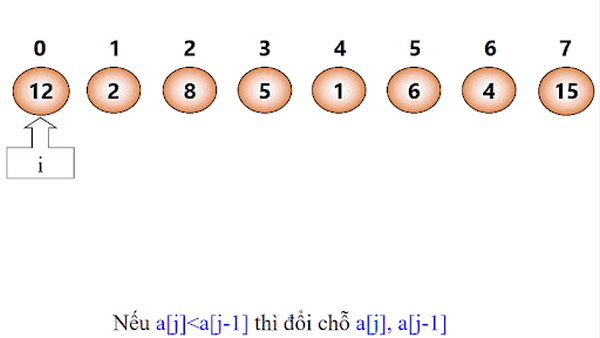
      if L[j] > L[j + 1] //nếu chúng không đúng thứ tự

        swap(L[j], L[j + 1]) //đổi chỗ chúng cho nhau

        has_swapped:= 1 //có đổi chỗ ít nhất một lần, danh sách chưa sắp xếp xong

      endif

    endfor  

    if has_swapped = 0 //nếu không có lần đổi chỗ nào, danh sách đã sắp xếp xong

      exit

    else //nếu có ít nhất một lần đổi chỗ, danh sách chưa sắp xếp xong

      i = i – 1

    endif

  enddo

endprocedure

Ghi chú: Nếu không sử dụng đến biến i, mỗi lần kiểm tra đều phải duyệt từ đầu đến cuối dãy.

Phân loại thuật toán sắp xếp

Ngoài Bubble Sort, chúng ta còn có thể tìm hiểu một vài thuật toán khác cũng vô cùng thông dụng. Thuật toán sắp xếp có thể chia thành hai loại:

• Sắp xếp ổn định: Là thuật toán mà sau khi tiến hành sắp xếp vị trí tương đối của các phần tử không bị thay đổi
• Sắp xếp so sánh: Là thuật toán mà trong quá trình thực hiện thuật toán ta phải tiến hành so sánh các khoá và đổi chỗ của các phần tử cho nhau. Đa số các thuật toán chúng ta thường dùng là sắp xếp so sánh, riêng sắp xếp đếm phân phối không được tính là sắp xếp so sánh.

Một số thuật toán sắp xếp khác

• Sắp xếp chèn (Insertion Sort) là thuật toán xử lý bằng cách chèn phần tử đang xét vào vị trí thích hợp của dãy số sẵn có sao cho dãy số vẫn duy trì được thứ tự vốn có.
• Sắp xếp chọn (Selection Sort) là phương pháp chọn ra phần tử bé nhất xếp vào vị trí thứ nhất và tiếp tục với toàn bộ các phần tử còn lại vào các vị trí tiếp theo.
• Shell Sort là một giải thuật sắp xếp mang lại hiệu quả cao nhờ dựa vào sắp xếp chèn (Insertion Sort). Giải thuật này tránh được tình trạng phải tráo đổi vị trí của hai phần tử xa nhau trong giải thuật sắp xếp chọn.
• Sắp xếp đếm phân phối là thuật toán sắp xếp bằng cách đếm số lần xuất hiện duy nhất trong mảng. Các số đếm này sau đó sẽ được xếp vào một mảng phụ và việc so sánh sẽ dựa vào mảng phụ này.
• Sắp xếp nhanh (Quick Sort) là một thuật toán theo tư tưởng chia để trị, thực hiện như sau: Chia dãy số có sẵn bằng cách chọn ra một phần tử chốt (pivot) và chuyển tất cả phần tử nhỏ hơn chốt về phía trước chốt và các phần tử lớn hơn chốt về phía sau chốt. Và ngược lại nếu sắp xếp dãy theo thứ tự nhỏ dần. Công việc sắp xếp này được thực hiện lặp đi lặp lại cho đến khi các dãy con chỉ còn một phần tử.

Ngoài các giải thuật trên còn có nhiều loại giải thuật khác được phát triển, cải tiến từ các loại giải thuật đã có. Giải thuật chèn, chọn thường được coi là cơ bản và các giải thuật còn lại được xếp vào loại cao cấp hơn. 

Hy vọng bài viết của chúng tôi đã cung cấp được cho bạn những kiến thức bổ ích và mới mẻ về lập trình và thuật toán sắp xếp. Để có thể học được những cách áp dụng, những bài học phù hợp hơn với bản thân mình, hãy liên hệ ngay với FPT Aptech để tìm cho mình những khoá học với đủ mọi trình độ dành riêng cho bạn.