Thuật toán Dijkstra có công năng chính của nó là thay thế con người tìm đường đi ngắn nhất mà chúng ta không thể tính toán bằng bộ não, ví dụ điển hình có thể là các app Google Map của Mỹ hay Baidu Map của Trung Quốc cũng một phần sử dụng thuật toán này. Vậy hãy cùng tìm hiểu chi tiết về thuật toán này và các vận dụng nhé.
Nội dung
Thuật toán tìm đường đi ngắn nhất Dijkstra là gì và lịch sử ra đời
Đây là thuật toán được ra đời bởi nhu cầu tìm kiếm giải pháp cho việc tìm kiếm đường đi từ thành phố này đến thành phố khác của con người một cách ngắn nhất. Nó được ra đời chính thức vào năm 1959 bởi nhà khoa học máy tính ông Dijkstra.
Thuật toán Dijkstra tìm đường đi ngắn nhất giải quyết bài toán đường đi ngắn nhất từ một điểm đến các điểm còn lại của đồ thị.
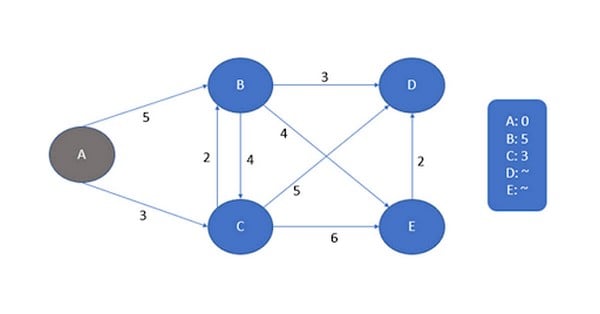
Ví dụ, để biểu diễn đường đi ngắn nhất từ thành phố A đến thành phố B, chúng ta dùng các đỉnh của đồ thị để thị phạm các thành phố và các cạnh để biểu diễn các đường nối giữa chúng. Trọng số các cạnh sẽ được xem như độ dài của các con đường, vì vậy mà chúng không âm, nhờ đó thuật toán sẽ chỉ ra con đường ngắn nhất.
Trọng số không âm các cạnh mang tính tổng thể hơn là khoảng cách hình học giữa 2 định, vì vậy thuật toán sẽ có tính chính xác cao hơn.
Dijkstra thường được ứng dụng trong bộ định tuyến với một chương trình con trong một hệ thống định vị toàn cầu hay còn gọi là GPS.
So sánh thuật toán dijkstra và bellman-ford cơ bản
Để so sánh 2 loại thuật toán tìm đường đi ngắn nhất, trước hết cần hiểu được định nghĩa của các loại thuật toán này ra sao. Về tổng thể, trong giới kỹ thuật tồn tại 3 dạng thuật toán tìm đường đi ngắn nhất:
- Thuật Bellman-Ford
- Thuật Dijkstra
- Thuật Floyd-Warshall.
Tuy nhiên, thuật toán Floyd còn dùng để tìm chu trình trong một đồ thị, do đó, sẽ không đề cập sâu trong bài viết này mà ta chỉ tập trung vào 2 thuật toán tìm đường đi ngắn nhất Dijkstra và Bellman-Ford.
Sơ lược về thuật toán Bellman-Ford và thao tác tìm đường đi ngắn nhất
Đây là thuật toán sử dụng nhằm giải quyết bài toán đường đi ngắn nhất một nguồn (single source), đồ thị trọng số có âm.
Ý tưởng của thuật toán được xét đến khi đồ thị không tồn tại trọng số âm, tức là đường đi ngắn nhất có tồn tại và luôn như thế.
Thuật toán này sẽ lặp lại nhiều lần và ở mỗi vòng lặp, chủ thể sẽ đi qua tất cả các cạnh (u,v) trên đồ thị. Các nhà nghiên cứu nhận xét rằng một đường đi ngắn nhất tùy ý sẽ không có điểm được đi lại thêm một lần nào nữa, như vậy đường đi ngắn nhất sẽ là N-1, trong đó N- 1 là vòng lặp thực hiện trong thực nghiệm.
Bellman-Ford thường được lưu ở dạng danh sách cạnh và có các lưu ý sau trong thuật toán:
- Định nghĩa W[u,v] là trọng số cạnh nối đỉnh u đến đỉnh v.
- Định nghĩa mảng D[u] là đường đi ngắn nhất từ s đến u.
- Độ phức tạp của thuật toán là O(N*M) trong một vòng lặp được thực hiện N – 1 lần và mỗi lần như vậy ta sẽ xử lý tất cả các cạnh trong đồ thị.
Mức độ xử lý tìm đường đi ngắn nhất của thuật toán khá đơn giản bằng cách truy vết từ đỉnh u theo mảng trace và ngược lại điểm bắt đầu S, code như sau:
vector<int> trace_path(vector<int> &trace, int S, int u) {
if (u != S && trace[u] == -1) return vector<int>(0); // không có đường đi
vector<int> path;
while (u != -1) { // truy vết ngược từ u về S
path.push_back(u);
u = trace[u];
}
reverse(path.begin(), path.end()); // cần reverse vì đường đi lúc này là từ u về S
return path;
}
Sơ lược thuật toán Dijkstra tìm đường đi ngắn nhất
Đây là thuật toán sử dụng nhằm giải quyết bài toán đường đi ngắn nhất một nguồn (single source), đồ thị trọng số không âm.
Ý tưởng bài toán cũng tương tự Bellman-Ford, thuật toán Dijkstra cũng tối giản đường đi bằng cách xét các cạnh và so sánh 2 đường đi sẵn có với đường qua cả 3 đỉnh.
Nguyên lý hoạt động bằng cách duy trì một tập hợp các đỉnh trong đó đã được biết chắc đường đi ngắn nhất. Qua từng bước, thuật toán sẽ chọn ra một đỉnh mà chắc chắn đã được tối ưu hóa cao nhất. Sau N bước, tất cả các đỉnh đều được chọn và mọi đường đi tìm được đều sẽ là ngắn nhất.
Dijkstra thường được lưu dưới dạng danh sách kề và có các lưu ý sau:
- D[u] là đường ngắn nhất từ s đến u.
- W[u,v] là trọng số cạnh trên đường đi từ u đến v.
- P[u] là mảng đánh dấu các đỉnh u với tất cả giá trị ban đầu đều là False.
- Độ phức tạp của thuật toán là O(N^2 + M)
Để tìm lại đường đi ngắn nhất từ S về u, ta sẽ truy vết từ đỉnh u theo mảng trace và về ngược lại S, code như sau:
vector<int> trace_path(vector<int> &trace, int S, int u) {
if (u != S && trace[u] == -1) return vector<int>(0); // không có đường đi
vector<int> path;
while (u != -1) { // truy vết ngược từ u về S
path.push_back(u);
u = trace[u];
}
reverse(path.begin(), path.end()); // cần reverse vì đường đi lúc này là từ u về S
return path;
}
Như vậy, thông qua sơ lược 2 thuật toán, bạn có thể phân biệt được Dijkstra và Bellman-Ford thông qua 4 yếu tố chính:
- Bài toán giải quyết vấn đề tìm đường đi ngắn nhất như thế nào
- Độ phức tạp ra sao
- Có sử dụng được cho trọng số âm hay không
- Có tìm được chu trình âm hay không.
Cách triển khai thuật toán Dijkstra Python cơ bản
Như đã biết, thuật toán Dijkstra được áp dụng với mục đích tìm đường đi ngắn nhất giữa các nút trong đồ thị. Công cụ này được sử dụng trong thực tiễn dưới các sản phẩm tìm được tự động giữa các vị trí thực tế, ví dụ như Google Maps là một sản phẩm của thuật toán Dijkstra.
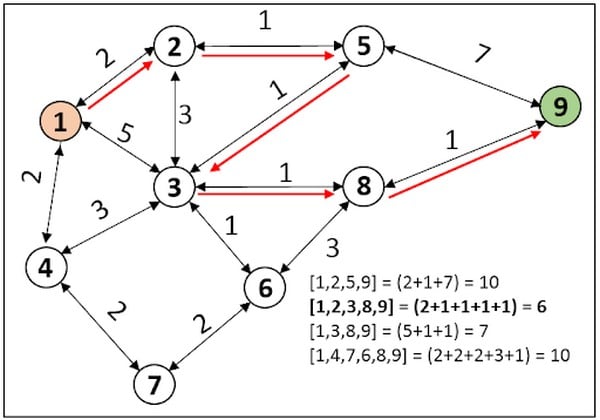
Ưu điểm của thuật toán Dijkstra là có thể giúp con người tìm ra con đường ngắn nhất cho dù giả định chi phí đi qua mỗi đường là khác nhau. Hơn nữa, thuật toán Dijkstra có một phương thức xử lý đặc biệt đó là giải quyết các nút gần nhất để có thể cho ra một số bước tắt để tìm đường đi ngắn nhất.
Sau đây là cách triển khai thuật toán Dijkstra C++ đơn giản nhất:
from head import *
from collections import defaultdict
def dijkstra(edges, strat_node, end_node):
g = defaultdict(list)
for start, end, weight in edges:
g[start].append((weight, end))
q, visited = [(0, strat_node,())], set()
while q:
(cost,v1,path) = heappop(q)
if v1 not in visited:
visited.add(v1)
path = (v1, path)
if v1 == end_node:
return (cost, path)
for c, v2 in g.get(v1, ()):
if v2 not in visited:
heappush(q, (cost+c, v2, path))
print (q)
return float(“inf”)
if __name__ == “__main__”:
edges = [
(“A”, “B”, 7),
(“A”, “D”, 5),
(“B”, “C”, 8),
(“B”, “D”, 9),
(“B”, “E”, 7),
(“C”, “E”, 5),
(“D”, “E”, 7),
(“D”, “F”, 6),
(“E”, “F”, 8),
(“E”, “G”, 9),
(“F”, “G”, 11)
]
print (“=== Dijkstra ===”)
print (“A >> G:”)
print (dijkstra(edges, “A”, “G”))
=== Dijkstra ===
Source code thuật toán dijkstra cần chú ý điều gì
Khi bắt đầu tìm hiểu thuật toán Dijkstra đa số các bạn đều sẽ thấy phức tạp bởi nó là tính toán của một chuỗi chu kỳ vòng lặp trông khá rắc rối, tuy nhiên, tóm tắt thuật toán có thể thực hiện 5 bước đơn giản sau:
- Bước 1: Đánh dấu đỉnh nguồn (đỉnh mở đầu) là $0$ và các đỉnh còn lại là “vô cùng”.
- Bước 2: Gọi đỉnh chưa xét với giá trị đánh dấu min là $C$ (current node).
- Bước 3: Mỗi đỉnh kề $N$ với đỉnh $C$, ta cộng giá trị đang đánh dấu của đỉnh $C$ với trọng số của cạnh nối đỉnh Current node cùng đỉnh kề, nếu kết quả nhỏ hơn giá trị đang đánh dấu ở $N$ thì ta cập nhật giá trị mới đó cho đỉnh.
- Bước 4: Đánh dấu đỉnh $C$ đã xét.
- Bước 5: Tiếp tục vòng lặp tại bước 2 cho đến khi không còn đỉnh chưa xét.
Ứng dụng thực tiễn của thuật toán Dijkstra trong đời sống hiện nay
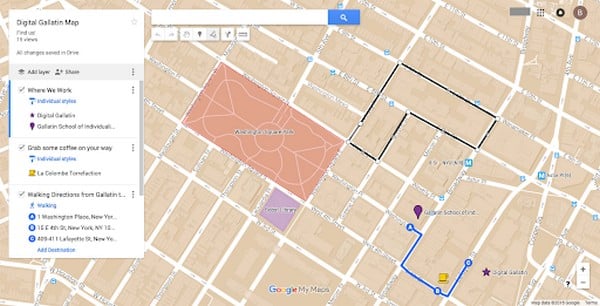
Ứng dụng tìm đường ngắn nhất trên bản đồ
Theo đó, các ứng dụng tìm kiếm đường đi và chỉ đường hiện nay đều sẽ hiện nhiều lựa chọn với các trị số thời gian để bạn lựa chọn ra con đường ngắn nhất từ điểm xuất phát đến điểm đến dựa trên những hiển thị và các yếu tố tác động từ vệ tinh, từ đó áp dụng thuật toán Dijkstra C++ để hiển thị đường.
Ứng dụng trong mạng xã hội
Các trang doanh nghiệp kinh doanh nhỏ lẻ hay các trang mạng xã hội có hướng dẫn đường đi cho người theo dõi cũng áp dụng thuật toán Dijkstra để nhúng đường đi của doanh nghiệp lên mạng xã hội. Qua đó, người dùng chỉ cần truy cập trang facebook của doanh nghiệp, sử dụng chức năng chỉ đường là sẽ tự động được tính toán và dẫn ra con đường ngắn nhất.
Ứng dụng trong hệ thống thông tin di động điện tử
Ngoài việc tìm đường đi thực tế, một số hệ thống thông tin di động còn ứng dụng thuật toán này để có thể truyền tải thông tin nhanh hơn khi có kết nối nội bộ giữa các đỉnh, các đỉnh này có thể là GPS hay Airdrop, miễn là có kết nối thì thuật toán sẽ tìm được đường nhanh nhất để truyền tải thông tin bạn muốn.
Bên cạnh đó, việc sử dụng internet cũng là điều kiện để các hacker sử dụng dấu vết của bạn, kết nối các đỉnh và truy tìm ra những thông tin được kết nối cũng như đường chính xác và ngắn nhất đến địa điểm mà bạn đang truy cập mạng.
Ứng dụng trong kỹ thuật của ngành hàng không vũ trụ
Tương tự hệ thống giao thông vận tải mặt đất, thuật toán Dijkstra cực kỳ hữu dụng khi các phi công phải dựa trên bản đồ hiển thị trong quá trình lái máy bay được tích hợp thông qua thuật toán, tránh việc tìm đường dựa trên cảm quan gây ra những sai sót nghiêm trọng đến tính mạng cũng như các hệ lụy nặng nề khác.
Tính chất của ngành hàng không là phải bay theo quỹ đạo được định sẵn bởi thuật toán, nếu bạn cố ý bay chệch đường bay được định sẵn, thuật toán sẽ trở nên lộn xộn và dễ vượt ngoài tầm kiểm soát.
Lời kết
Qua những thông vừa rồi được nêu trên đây về thuật toán Dijkstra được áp dụng nhiều trong các cuộc thi lập trình, ứng dụng khoa học công nghệ đời sống để giải quyết bài toán tìm đường đi ngắn nhất một cách hiệu quả. Hy vọng đã gỡ rồi được phần nào cho các bạn lập trình viên đang học đến thuật toán này.
| FPT Aptech trực thuộc Tổ chức Giáo dục FPT có hơn 25 năm kinh nghiệm đào tạo lập trình viên quốc tế tại Việt Nam, và luôn là sự lựa chọn ưu tiên của các sinh viên và nhà tuyển dụng. |



