Quy hoạch động là một trong những thuật toán được sử dụng rất nhiều trong các cuộc thi code. Hơn một nửa bài thi trong cuộc thi code đều dùng đến thuật toán này để giải nhanh nhất. Nếu bạn chuẩn bị bước vào kỳ thi này thì đừng bỏ qua bài viết này. Hãy cùng Aptech theo dõi bài viết dưới đây để hiểu rõ hơn về thuật toán này nhé!
Nội dung
Quy hoạch động là gì?
Quy hoạch động (dynamic programming) là kỹ thuật trong lập trình giúp đơn giản hóa hiệu quả việc chia bài toán lớn thành các bài toán con chồng chéo và cấu trúc con tối ưu. Những bài toán này thường có nhiều nghiệm đúng và mỗi nghiệm có một giá trị đánh giá. Do đó, cần tính toán nhiều lần và sử dụng lời giải của các bài toán con để tìm ra đáp án cho bài toán ban đầu.
Khi bạn muốn giải quyết một bài toán một cách nhanh nhất thì thuật toán này là một cách giải giúp tối ưu thời gian. Quy hoạch động này bao gồm bốn bước như sau:
- Bước 1: Đặc trưng hóa cấu trúc của lời giải tối ưu.
- Bước 2: Định nghĩa giá trị của lời giải tối ưu một cách đệ quy.
- Bước 3: Tính trị của lời giải tối ưu theo kiểu từ dưới lên hoặc trên xuống.
- Bước 4: Xây dựng lời giải tối ưu từ những thông tin đã được tính toán trên.
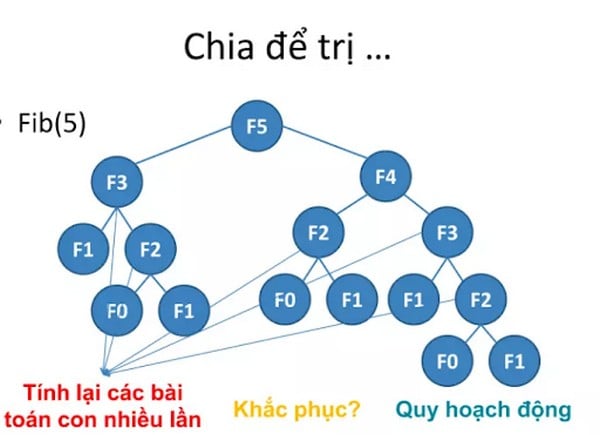
Thay vì gọi đệ quy, thuật toán sẽ tính toán lời giải của các bài toán con trước tiên và lưu vào mảng bộ nhớ. Tiếp theo, sẽ dùng lời giải của bài toán con trong mảng đã tính trước đó để giải bài toán lớn theo công thức truy hồi. Công thức truy hồi là công thức thể hiện quan hệ giữa các bước trong một bài toán và kết quả của bước sau nhờ vào kết quả của các bước trước đó.
Thuật toán này với ưu điểm chính là tiết kiệm thời gian tính toán thì cũng có một vài nhược điểm. Đầu tiên, việc tìm ra công thức truy hồi hay phân rã bài toán lớn yêu cầu phải suy nghĩ và phân tích thật kỹ càng. Điều này sẽ giúp bạn tránh được sự sai sót cũng như rủi ro phải tính lại từ đầu. Thứ hai là khó xử lý dữ liệu khi bảng lưu trữ yêu cầu mảng hai hoặc ba chiều. Cuối cùng, không phải bài toán tối ưu nào cũng có thể áp dụng giải bằng phương pháp này.
Bên cạnh đó, một bài toán tối ưu cũng có một số đặc điểm cần lưu ý dưới đây:
- Cần phân tách bài toán lớn thành nhiều bài toán con và kết hợp lời giải của các bài toán con để giải của bài toán lớn.
- Bản chất của thuật toán là giải tất cả các bài toán con. Quy hoạch động không thể tiến hành được nếu không gian lưu trữ không đủ để phối hợp.
Khi nào nên áp dụng thuật toán quy hoạch động?
Điểm quyết định trong khi giải thuật toán này là cần tìm ra được công thức truy hồi cho từng trường hợp bài toán. Đối với một số bài toán thì dễ dàng có nhiều cách giải và giải bằng quy hoạch này nhưng chưa hẳn là giải pháp tối ưu. Mỗi bài toán là mỗi kiểu khó khác nhau, không có một công thức chung cho tất cả các bài toán đó được.
Vậy khi nào chúng ta nên áp dụng đến thuật toán hay ho này? Thường bài toán có hai tính chất này là bạn có thể sử dụng thuật toán quy hoạch động vào. Đó chính là bài toán con gối nhau và cấu trúc con tối ưu.
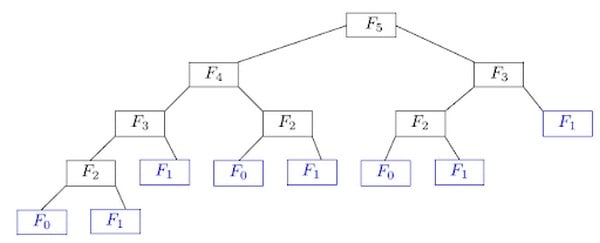
Bài toán con gối nhau
Bài toán con gối nhau là bài toán nhỏ hơn và được chia từ bài toán ban đầu ra. Việc sử dụng lặp lại nhiều lần này, thuật toán sẽ lưu kết quả mà không cần tính lại, giúp bạn tiết kiệm rất nhiều thời gian. Việc giải một bài toán con nhiều lần thì không thể tránh khỏi việc trùng lời giải của các bài toán con.
Khi các bài toán con không gối nhau thì việc áp dụng thuật toán này cũng bằng không. Quy hoạch động không thể tối ưu được với thuật toán tìm kiếm nhị phân. Lý do vì khi chia bài toán lớn thành các bài toán nhỏ và mỗi bài toán chỉ cần giải một lần mà không được gọi lại.
Bài toán tính Fibonacci là ví dụ rất điển hình của bài toán con gối nhau. Bằng cách cộng fibonacci thứ n-1 và n-2 sẽ tính được số fibonacci thứ n. Bài toán con của số fibonacci thứ n chính là bài toán tính fibonacci n-1 và n-2. Công thức tính toán số Fibonacci được tính như sau:
def fib(n):
if n <= 1:
return n
return fib(n -1) + fib(n – 2)
Đây chính là một trong số những giải pháp cực kỳ hiệu quả có thể tối ưu hóa quá trình tính toán này. Trước khi tiến hành tính những bài lớn thì mỗi bài toán con sẽ được lưu lại. Nhờ đó, mà việc tính toán giảm đi đáng kể, mỗi bài toán con chỉ cần tính đúng một lần. Nhờ đó mà thuật toán này được sử dụng rất nhiều trong các cuộc thi lập trình giúp các thí sinh giảm đáng kể thời gian tính toán.
Cấu trúc con tối ưu
Bài toán có cấu trúc con tối ưu là gì? Cấu trúc con tối ưu chính là tập hợp các lời giải tối ưu từ các bài toán con để tìm ra lời giải bài toán lớn. Bài toán có cấu trúc con tối ưu có thể dễ dàng tính toán hoặc có khi không cần phải tính toán nữa. Các bài toán con tối ưu có thể sử dụng công thức truy hồi đưa vào thuật toán để tìm ra đáp án cuối cùng cho bài toán.
Cấu trúc con tối ưu với quy trình ba bước mà bạn nên nắm rõ để có thể giải một bài toán nhanh chóng nhất:
- Bước 1: Từ bài toán lớn chia thành các bài toán con nhỏ hơn.
- Bước 2: Sử dụng phương pháp đệ quy để giải các bài toán con tối ưu.
- Bước 3: Lấy kết quả tối ưu đã tính để có thể dễ dàng tìm lời giải tối ưu cho bài toán lớn trên.
Bài toán có cấu trúc con tối ưu rất quan trọng, bởi nó cho phép bạn dựa vào các bài toán con đã giải để có lời giải cho bài toán lớn. Chúng ta sẽ không thể nào áp dụng thuật toán quy hoạch động nếu bài toán không có tính chất này.
- Giải mà về thuật toán Dijkstra tìm đường đi ngắn nhất
- Giải đáp: Lập trình viên lương bao nhiêu? Có cao hay không?
Các phương pháp
Trong quy hoạch động, chúng ta có thể sử dụng một trong hai cách để lưu trữ dễ dàng các giá trị đã tính như sau:
Phương pháp từ trên xuống (phương pháp ghi nhớ )
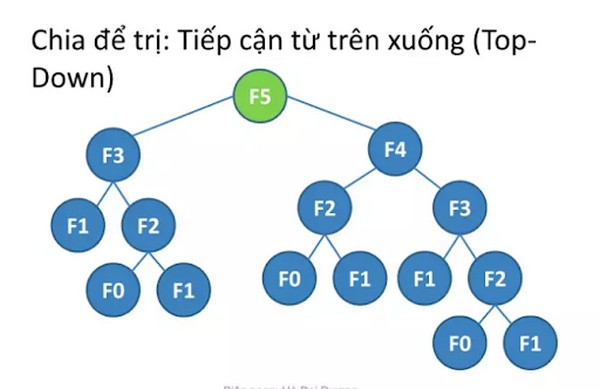
Với phương pháp này, bạn sẽ bắt đầu giải bài toán từ trên xuống. Bằng cách lặp đệ quy để giải bài toán lớn hơn, từ đó tìm ra lời giải cho các bài toán con. Các bài toán con này được giải và lưu kết quả vào bộ nhớ. Việc ghi nhớ câu trả lời này sẽ giúp bạn giải quyết vấn đề con mà không tốn quá nhiều thời gian.
Phương pháp từ dưới lên (phương pháp lập bảng )
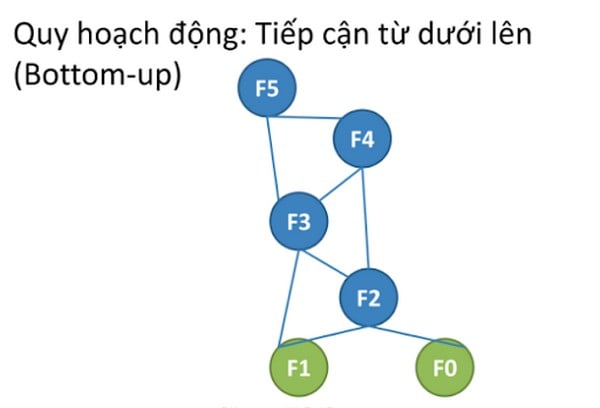
Phương pháp lập bảng này trái ngược hoàn toàn với phương pháp ghi nhớ. Cách tiếp cận này sẽ không dùng đệ quy và giải quyết bài toán con liên quan từ dưới lên. Bạn trực tiếp giải tất cả bài toán nhỏ và điền vào bảng N chiều. Sau đó, dùng kết quả trong bảng để tìm ra dần lời giải cho bài toán ban đầu. Cách tiếp cận này hiệu quả và được sử dụng nhiều hơn phương pháp ghi nhớ bởi nó sẽ không làm tốn bộ nhớ và số lần gọi hàm.
Thông qua bài viết với những thông tin chi tiết về quy hoạch động, hy vọng các bạn đã nắm rõ được khái niệm và hiểu được bản chất của thuật toán này. Nếu bạn đang muốn tìm hiểu thêm liên quan đến kiến thức học lập trình hay muốn trở thành lập trình viên tương lai thì có thể liên hệ với FPT Aptech nhé!
| FPT Aptech trực thuộc Tổ chức Giáo dục FPT có hơn 25 năm kinh nghiệm đào tạo lập trình viên quốc tế tại Việt Nam, và luôn là sự lựa chọn ưu tiên của các sinh viên và nhà tuyển dụng. |




